직각삼각형 계산기
직각삼각형이란
기하학에서 직각삼각형은 한 각이 직각인 삼각형이다. 피타고라스 정리에 의해 삼각형의 두 변의 길이가 주어졌을때 나머지 한변의 길이를 계산할 수 있다. 직각삼각형의 외심은 직각삼각형의 빗변의 중점에 있다. 이것은 직각삼각형의 빗변의 중점에서 세 꼭짓점까지의 거리가 같다는 것을 의미한다.
직각 삼각형의 합동조건
직각삼각형은 하나의 각이 90도로 정해져 있기 때문에 아래와 같은 두가지의 합동 조건이 있다. RHA합동: 빗변의 길이와 한 각의 크기가 같으면 두 직각삼각형은 합동이다. AAS합동과 같은 논리이다. RHS합동: 빗변의 길이와 한 변의 길이가 같으면 두 직각삼각형은 합동이다. 피타고라스 정리로부터 보일 수도 있다.
밑변과 높이를 알고 있을때
직각삼각형의 빗변을 구하는 공식
직각삼각형의 ab각(θ)을 구하는 공식
직각삼각형의 넓이를 구하는 공식
밑변과 빗변을 알고 있을때
직각삼각형의 ab각(θ)을 구하는 공식
직각삼각형의 높이를 구하는 공식
직각삼각형의 넓이를 구하는 공식
밑변과 각도를 알고 있을때
직각삼각형의 빗변을 구하는 공식
직각삼각형의 높이를 구하는 공식
직각삼각형의 넓이를 구하는 공식
빗변과 높이를 알고 있을때
직각삼각형의 ab각(θ)을 구하는 공식
직각삼각형의 높이를 구하는 공식
직각삼각형의 넓이를 구하는 공식
각이 30도, 60도 인경우
한 각이 30도 또는 60도인 직각 삼각형은 특별한 유형의 직각 삼각형이다. 이 삼각형의 세 각은 30도, 60도, 90도가 된다. 이 직각 삼각형의 길이의 비율은 1(높이) : √3(밑변) : 2(빗변) 이 된다. 이것은 빗변의 길이가 짧은 면의 2배이고 긴 면는 짧은 면의 3배의 제곱근임을 의미한다.
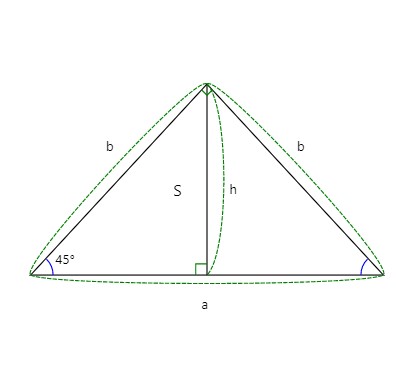
각이 45도 인경우
한 각이 45도인 직각 삼각형 또한 특별한 유형의 직각 삼각형이다. 이 삼각형의 세 각은 45도, 45도, 90도가 된다. 그러므로 직각 이등변 삼각형과 이등변 삼각형의 성경또한 가지고 있다. 이 직각 삼각형의 길이의 비율은 1(높이) : 1(밑변) : √2(빗변) 이 된다. 이것은 빗변의 길이가 짧은 면의 2배의 제곱근임을 의미한다.
피타고라스 정리
피타고라스 정리(Pythagorean theorem)는 기원전 570년경에 태어난 그리스 철학자 피타고라스의 이름을 따서 붙여졌다. 직각 삼각형의 두 직각변 a 와 h 를 각각 한 변으로 하는 정사각형 면적의 합은 빗변 b를 한 변으로 하는 정사각형의 면적과 같다는 것이다.
피타고라스 공식
카테고리내의 계산기들
정삼각형
정삼각형의 한변의 길이, 높이, 면적중 주어진 한 값으로 나머지 높이, 한변의 길이 , 둘레 면적을 계산하는 방법을 계산. 정삼각형은 동일한 길이의 3개의 선분과 3개의 점으로 이루어진 다각형을 말한다.
정삼각형 계산기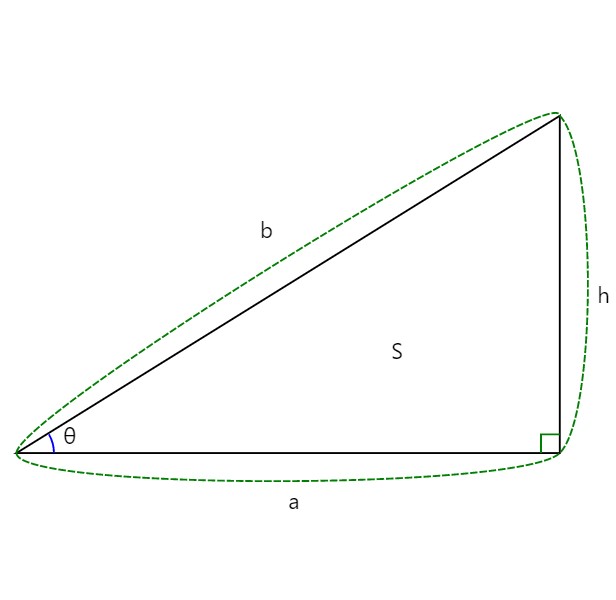
직각이등변삼각형
직각 이등변 삼각형(Isosceles right triangle)은 두변의 길이가 같으면서 길이가 서로 같은 두 변 사이의 각이 90도인 삼각형을 말한다.
직각이등변삼각형 계산기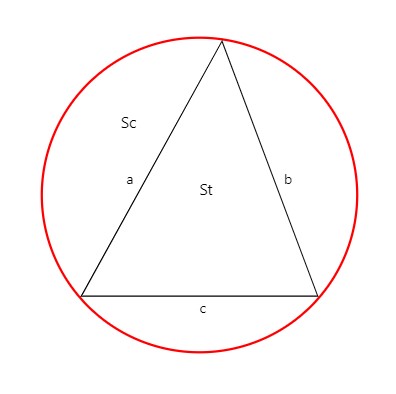
외접원
기하학에서 삼각형은 꼭지점이 접하는 외접원을 그릴 수 있다는 점에서 수학/기하학 문제에서 자주 등장한다. 삼각비와 원의 성격을 이용해서 삼각형의 넓이 , 원의 넓이 그리고 이 둘의 면적 비율등을 계산 할 수 있다.
외접원 계산기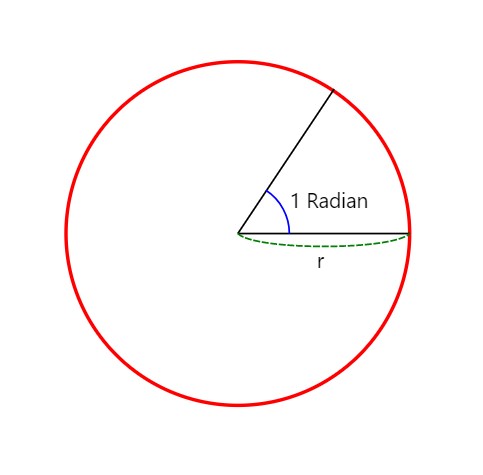
각도(deg)레디안(rad)변환
직각삼각형의 계산을 위해 필요한 각도(degree)와 라디안(radian) 값의 변환 계산기. 변환방법 설명
각도(deg)레디안(rad)변환 계산기

원의 넓이와 둘레
원의 넓이를 구하는 방법은 다음과 같다. [1. 반지름을 구한다] [2. 반지름을 두번 곱한다] [3. 반지름을 두번 곱한 값에 원주율(3.14)을 곱한다]
원의 넓이와 둘레 계산기
타원의 넓이와 둘레
타원의 넓이와 둘레를 구하는 방법. 타원의 넓이는 장축과 단축 그리고 파이를 곱한값이다. 타원의 둘레는 장축의 제곱과 단축의 제곱의 합에 2를 곱하고 제곱근해서 파이를 곱해주면된다. .
타원의 넓이와 둘레 계산기